5. Maximum size rectangle binary sub-matrix [Google]

5. Maximum size rectangle binary sub-matrix [Google]

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing all ones and return its area.

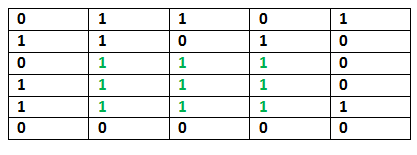
Example :

Input : [[1, 1, 1], [0, 1, 1], [1, 0, 0]]
Return  : 4 

Input:
[
  [1, 0, 1, 0, 0],
  [1, 0, 1, 1, 1],
  [1, 1, 1, 1, 1],
  [1, 0, 0, 1, 0]
]
Return: 6

To solve this problem, developers need to understand few concepts:

1. The bruteforce approach is to look at all pairs of (i,j) to (k,l) and check if its filled with 1s. This approach however is O(NNNNN²) = O(N⁶). [ N⁴ ways to choose i,j,k,l and then N² elements in the square ].

Can you optimize this approach if you had additional space to store results for your previous calculations ?
Maybe if you knew the result for (i, j) to (k, l — 1) or (i, j) to (k — 1, l) or both ?

We can improve from N⁶ by storing in dp[i][j][k][l] if (i,j) to (k,l) is all filled with 1.
dp[i][j[k][l] = 1 iff dp[i][j][k][l-1] = 1 && dp[i][j][k-1][l] = 1 and matrix[k][l] = 1.

Now we can improve this further. What if with every (i,j) we stored the length of 1s in the same row i starting from (i,j).
Can we move down in the column j from row i and determine the largest rectangle without having to visit all cells ?
2. If you notice, laying out max_x[i][j] helps you make histograms in every row. Then the problem becomes of finding the maximum area in histograms ( which we can solve using Stacks and Queues ) in O(n). This would lead to an O(N²) solution. We strongly suggest you to explore the O(N²) solution as well.

Problem: Maximum size rectangle binary sub-matrix with all 1s

How to Approach this problem?

Congratulations! You just solved a problem that was asked in interviews at Microsoft , Facebook & Google.

Thanks for reading this article, keep learning & growing.

Github: https://github.com/charlieInDen/InterviewQuestions-Swift/